Um die Vorstellung über die DNA etwas bildhaft zu machen, wurden viele Vergleiche vorgeschlagen, die alle beweisen, dass wir die Größenverhältnisse nicht begreifen können. Hier folgt noch ein Vergleich aus dem Buch Information, Der Schlüssel zum Leben, von W. Gitt, S. 411: „Würden wir nur ein Milligramm (1mg = 10-3 g) des DNS-Materials nehmen und läge diese verdrillte Strickleiter als einziger Strang vor, dann entspräche das fast der Länge von der Erde bis zum Mond!“
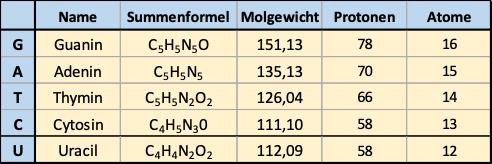
Der genetische Code selbst benutzt 4 Nukleobasen, die jeweils einzeln 2 Bit Information speichern. Da die gespeicherte Information paarweise angeordnet ist, kommt die Besonderheit hinzu, dass jede Informations-Einheit auch doppelt gespeichert wird. Eine Informations-Einheit wird in Form eines sogenannten Basen-Paares gespeichert, das zugleich auch der physikalischen Stabilisierung der Doppel-Helix dient. An dieser Stelle sind wir bei dem äußerst wichtigen Thema Redundanz (mehrfache Information) angelangt.
DNA
Die Redundanz des genetischen Codes
Die Redundanz einer Information erlangt umso mehr an Bedeutung, als die Information etwas sehr Wertvolles repräsentiert. Das heißt, dass sensible Daten nicht nur vor unerwünschten Zugriffen geschützt werden müssen, sondern auch vor Verlust oder Veränderung. Im Falle einer Störung gehen oft Daten verloren oder werden mit unerwünschten Daten vermischt. In Zell-Prozessen kommt es in seltenen Fällen zu einem Kopierfehler, der böse Folgen haben könnte. Ein Kopierfehler im Zell- Prozess ist jedoch kein Grund zu Besorgnis. Einmal weil die genetische Information selbst ein hohes Maß an Redundanz aufweist. Wie bereits erwähnt, ist für jede einzelne Informations-Einheit ein Basen-Paar (bp) als Speicherplatz reserviert – also eine doppelte Speicherung. Eine Reihe von Kopier-Fehlern kann allein mit Hilfe einer Auswertung der doppelten Speicherung behoben werden. Darüber hinaus gibt es eine ganze Reihe von sehr spezifischen Reparatur-Systemen, die jeden „Kopier-Prozess“ begleiten. Bis auf einige absolute Ausnahmen werden von diesen Systemen alle Fehler vollautomatisch korrigiert. Und letztlich ist der Code selbst so beschaffen, dass eine Vielzahl von Kopierfehlern, falls diese denn nicht behoben worden wären, keinerlei Auswirkungen hätten.
Wir wissen, dass der genetische Code mit nur 4 Buchstaben geschrieben wird. Ist das nun eine günstige oder eher ungünstige Menge an Zeichen? Falls es darum ginge, so wenige verschiedene Zeichen wie möglich zu benutzen, dann wäre das Morse-Alphabet mit seinen zwei Buchstaben schon besser. Doch die Anwendung eines Systems mit wenigen verschiedenen Zeichen hat den entscheidenden Nachteil, dass die Botschaft, die man damit übermitteln will, viel länger wird, das heißt aus viel mehr Zeichen besteht, als wenn man mehr verschiedene Buchstaben zur Verfügung hat. Es geht darum, einen Kompromiss zu finden. Alle geschaffenen lebenden Systeme existieren auf der Grundlage von Kompromissen, weil es in der Biologie fast nie darum geht, eine Maximierung eines Systems zu erreichen, sondern immer um dessen Optimierung. Dabei behalten wir im Sinn, dass in der Regel jede Maximierung eines Systems an der Position A eine Verschlechterung an der Position X im System nach sich zieht. Daher ist die Optimierung der biologischen Systeme die Hauptstrategie des Designers.
Grundsätzlich gilt in der Informatik, dass ein Zeichensystem möglichst große Informationsmengen mit Hilfe einer möglichst kleinen Menge von Zeichen übermitteln soll. Dabei sind Nebenbedingungen zu beachten, die letztlich zur Festlegung des Zeichensystems beitragen. Im Falle der genetischen Information haben wir es fraglos mit großen Informationsmengen zu tun. Das zwingt zum Ersten dazu, das Speichervolumen zu minimieren. Aber wir haben bereits erörtert, dass die Datenstabilität und die Sicherheit der Weitergabe von Information die höchste Priorität im Zell-Prozess haben müssen. Es muss also der beste Kompromiss zwischen geringem Speichervolumen, hoher Stabilität und Datensicherheit und Geschwindigkeit der Verarbeitung im Zell-Prozess und nicht zuletzt auch der energetischen Effizienz gefunden werden. Das Kopieren jedes einzelnen Gens in der Zelle kostet Energie.
So eigenartig es klingen mag, die Ökonomie der Zell-Prozesse ist für den Designer bei der Auswahl des Zeichensystems ein wesentliches Kriterium. Wir werden jetzt in einer Kurzfassung einmal untersuchen, warum genau das Zeichensystem, das wir in Zell-Prozessen antreffen, in der Tat das effizienteste für irdisches Leben ist. Dabei machen wir nur zwei Grundannahmen, die darin bestehen, dass für die Realisierung von Leben auf der Erde 20 verschiedene Aminosäuren notwendig sind und dass die Helix aus 2 Strängen (Doppel-Helix) und nicht aus 3 Strängen bestehen sollte.
Aus diesen Grundannahmen können wir nun die Anzahl der zu codierenden Zeichen ableiten. Wir gehen davon aus, dass wir neben diesen 20 Code-Zeichen zusätzlich ein paar Operations-Zeichen benötigen. Damit erhalten wir die Anzahl von etwa 25 verschiedenen Codes, die wir benötigen. Bei völliger Wahlfreiheit könnte man nun ein Zeichensystem einsetzen, das genauso viele Zeichen bereitstellt, wie wir unterschiedliche Codes benötigen. Doch die Realität der Umsetzung offenbart eine Überraschung.
Nehmen wir an, wir wollen die 26 Buchstaben unseres Alphabetes in ein Code-System umsetzen. Wir gehen davon aus, dass wir einfach 26 verschiedene Zeichen erzeugen und das Code-System ist fertig. Die Frage ist jedoch, wie erzeugt man die 26 verschiedenen Zeichen. Mit Papier und Bleistift ist das keine Schwierigkeit, denn wir müssen nur die verschiedenen Buchstaben aufschreiben. Sobald wir es aber einer Maschine mitteilen wollen, zeigt sich das Problem. Die bekannteste Maschine, die mit einem Buchstaben-Code arbeitet, ist der PC und da können wir uns auch anschauen, wie der Buchstaben-Code anfänglich realisiert wurde.
Der PC hat, ähnlich wie die Zellen von Lebewesen, seine eigenen Randbedingungen, die bei der Realisierung von Codes jeder Art zwingend beachtet werden müssen. Die wichtigste ist, dass die zum Bau eines PC verfügbaren Bauelemente grundsätzlich nur 2 verschiedene Buchstaben oder Zeichen kennen, nämlich die Null und die Eins. Natürlich ist es keine Hürde mit nur diesen zwei Buchstaben eine unbegrenzte Anzahl von Zeichen zu erzeugen. Das Einzige, was man tun muss, ist, mehrere Grund-Buchstaben nacheinander oder quasi parallel zu benutzen, um einen größeren Vorrat an verschiedenen ‚Zeichen‘ bereitzustellen. Und so wurde schon ganz zeitig in der Entwicklungs-Phase der ersten Rechensysteme das Byte als eine Informationsgröße eingeführt, das aus 8 der kleinsten Informationseinheiten zusammengesetzt ist. Das Byte kann im Sinne der theoretischen Informatik auch als Wort bezeichnet werden, das eine Wortlänge von 8 Bit hat.
Mit einem Byte lassen sich nun 256 verschiedene Zustände codieren. Das reicht für jedes Alphabet aus und es bleiben viele Codes für die nötigen Steuerungen im Zusammenhang mit der Verarbeitung einer Information übrig. Um nur einige zu nennen, sei der Code für Zeilenende oder die Codes für Satzzeichen und Ziffern als auch für die Doppellaute und Sonderzeichen erwähnt.
Für den genetischen Code musste ein ähnliches Verfahren gefunden werden, um die gewünschten mehr als 20 Codierungen bereitzustellen. Die Anzahl der Buchstaben ist zwar auf der Grundlage von chemischen Zeichen nicht so stark eingeschränkt, wie im Falle der Schaltkreise für den PC, wo es eben nur zwei „Buchstaben“ gibt, doch je mehr verschiedene chemische Grund-Buchstaben existieren, umso komplexer werden die Decodierungs-Prozesse, weil die Vielzahl von „Buchstaben“ kompliziertere Erkennungs-Systeme erfordert. Für die Zell-Prozesse wurde die optimale Anzahl von 4 Buchstaben gewählt.
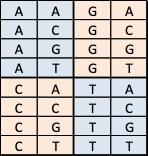
Es bleibt also die Frage: Wie viele Buchstaben der vier Grund-Buchstaben müssen kombiniert werden, um den Anforderungen zu entsprechen? Nehmen wir jeweils 2 der 4 Buchstaben und bilden ein „Wort“, so könnten wir insgesamt 4 mal 4 verschiedene solche „Worte“ bilden. Doch mit 16 verschiedenen Code-Worten könnten wir nicht alle 20 erforderlichen Aminosäuren codieren. Die folgende Tabelle zeigt einmal die 16 Möglichkeiten, die es gibt, jeweils 2 Buchstaben aus dem Vorrat von 4 Buchstaben (A, C, G, T) zu kombinieren, also Code-Worte aus 2 Buchstaben (2 Spalten der Tabelle) zu generieren.
Die Redundanz einer Information erlangt umso mehr an Bedeutung, als die Information etwas sehr Wertvolles repräsentiert. Das heißt, dass sensible Daten nicht nur vor unerwünschten Zugriffen geschützt werden müssen, sondern auch vor Verlust oder Veränderung. Im Falle einer Störung gehen oft Daten verloren oder werden mit unerwünschten Daten vermischt. In Zell-Prozessen kommt es in seltenen Fällen zu einem Kopierfehler, der böse Folgen haben könnte. Ein Kopierfehler im Zell- Prozess ist jedoch kein Grund zu Besorgnis. Einmal weil die genetische Information selbst ein hohes Maß an Redundanz aufweist. Wie bereits erwähnt, ist für jede einzelne Informations-Einheit ein Basen-Paar (bp) als Speicherplatz reserviert – also eine doppelte Speicherung. Eine Reihe von Kopier-Fehlern kann allein mit Hilfe einer Auswertung der doppelten Speicherung behoben werden. Darüber hinaus gibt es eine ganze Reihe von sehr spezifischen Reparatur-Systemen, die jeden „Kopier-Prozess“ begleiten. Bis auf einige absolute Ausnahmen werden von diesen Systemen alle Fehler vollautomatisch korrigiert. Und letztlich ist der Code selbst so beschaffen, dass eine Vielzahl von Kopierfehlern, falls diese denn nicht behoben worden wären, keinerlei Auswirkungen hätten.
Wir wissen, dass der genetische Code mit nur 4 Buchstaben geschrieben wird. Ist das nun eine günstige oder eher ungünstige Menge an Zeichen? Falls es darum ginge, so wenige verschiedene Zeichen wie möglich zu benutzen, dann wäre das Morse-Alphabet mit seinen zwei Buchstaben schon besser. Doch die Anwendung eines Systems mit wenigen verschiedenen Zeichen hat den entscheidenden Nachteil, dass die Botschaft, die man damit übermitteln will, viel länger wird, das heißt aus viel mehr Zeichen besteht, als wenn man mehr verschiedene Buchstaben zur Verfügung hat. Es geht darum, einen Kompromiss zu finden. Alle geschaffenen lebenden Systeme existieren auf der Grundlage von Kompromissen, weil es in der Biologie fast nie darum geht, eine Maximierung eines Systems zu erreichen, sondern immer um dessen Optimierung. Dabei behalten wir im Sinn, dass in der Regel jede Maximierung eines Systems an der Position A eine Verschlechterung an der Position X im System nach sich zieht. Daher ist die Optimierung der biologischen Systeme die Hauptstrategie des Designers.
Grundsätzlich gilt in der Informatik, dass ein Zeichensystem möglichst große Informationsmengen mit Hilfe einer möglichst kleinen Menge von Zeichen übermitteln soll. Dabei sind Nebenbedingungen zu beachten, die letztlich zur Festlegung des Zeichensystems beitragen. Im Falle der genetischen Information haben wir es fraglos mit großen Informationsmengen zu tun. Das zwingt zum Ersten dazu, das Speichervolumen zu minimieren. Aber wir haben bereits erörtert, dass die Datenstabilität und die Sicherheit der Weitergabe von Information die höchste Priorität im Zell-Prozess haben müssen. Es muss also der beste Kompromiss zwischen geringem Speichervolumen, hoher Stabilität und Datensicherheit und Geschwindigkeit der Verarbeitung im Zell-Prozess und nicht zuletzt auch der energetischen Effizienz gefunden werden. Das Kopieren jedes einzelnen Gens in der Zelle kostet Energie.
So eigenartig es klingen mag, die Ökonomie der Zell-Prozesse ist für den Designer bei der Auswahl des Zeichensystems ein wesentliches Kriterium. Wir werden jetzt in einer Kurzfassung einmal untersuchen, warum genau das Zeichensystem, das wir in Zell-Prozessen antreffen, in der Tat das effizienteste für irdisches Leben ist. Dabei machen wir nur zwei Grundannahmen, die darin bestehen, dass für die Realisierung von Leben auf der Erde 20 verschiedene Aminosäuren notwendig sind und dass die Helix aus 2 Strängen (Doppel-Helix) und nicht aus 3 Strängen bestehen sollte.
Aus diesen Grundannahmen können wir nun die Anzahl der zu codierenden Zeichen ableiten. Wir gehen davon aus, dass wir neben diesen 20 Code-Zeichen zusätzlich ein paar Operations-Zeichen benötigen. Damit erhalten wir die Anzahl von etwa 25 verschiedenen Codes, die wir benötigen. Bei völliger Wahlfreiheit könnte man nun ein Zeichensystem einsetzen, das genauso viele Zeichen bereitstellt, wie wir unterschiedliche Codes benötigen. Doch die Realität der Umsetzung offenbart eine Überraschung.
Nehmen wir an, wir wollen die 26 Buchstaben unseres Alphabetes in ein Code-System umsetzen. Wir gehen davon aus, dass wir einfach 26 verschiedene Zeichen erzeugen und das Code-System ist fertig. Die Frage ist jedoch, wie erzeugt man die 26 verschiedenen Zeichen. Mit Papier und Bleistift ist das keine Schwierigkeit, denn wir müssen nur die verschiedenen Buchstaben aufschreiben. Sobald wir es aber einer Maschine mitteilen wollen, zeigt sich das Problem. Die bekannteste Maschine, die mit einem Buchstaben-Code arbeitet, ist der PC und da können wir uns auch anschauen, wie der Buchstaben-Code anfänglich realisiert wurde.
Der PC hat, ähnlich wie die Zellen von Lebewesen, seine eigenen Randbedingungen, die bei der Realisierung von Codes jeder Art zwingend beachtet werden müssen. Die wichtigste ist, dass die zum Bau eines PC verfügbaren Bauelemente grundsätzlich nur 2 verschiedene Buchstaben oder Zeichen kennen, nämlich die Null und die Eins. Natürlich ist es keine Hürde mit nur diesen zwei Buchstaben eine unbegrenzte Anzahl von Zeichen zu erzeugen. Das Einzige, was man tun muss, ist, mehrere Grund-Buchstaben nacheinander oder quasi parallel zu benutzen, um einen größeren Vorrat an verschiedenen ‚Zeichen‘ bereitzustellen. Und so wurde schon ganz zeitig in der Entwicklungs-Phase der ersten Rechensysteme das Byte als eine Informationsgröße eingeführt, das aus 8 der kleinsten Informationseinheiten zusammengesetzt ist. Das Byte kann im Sinne der theoretischen Informatik auch als Wort bezeichnet werden, das eine Wortlänge von 8 Bit hat.
Mit einem Byte lassen sich nun 256 verschiedene Zustände codieren. Das reicht für jedes Alphabet aus und es bleiben viele Codes für die nötigen Steuerungen im Zusammenhang mit der Verarbeitung einer Information übrig. Um nur einige zu nennen, sei der Code für Zeilenende oder die Codes für Satzzeichen und Ziffern als auch für die Doppellaute und Sonderzeichen erwähnt.
Für den genetischen Code musste ein ähnliches Verfahren gefunden werden, um die gewünschten mehr als 20 Codierungen bereitzustellen. Die Anzahl der Buchstaben ist zwar auf der Grundlage von chemischen Zeichen nicht so stark eingeschränkt, wie im Falle der Schaltkreise für den PC, wo es eben nur zwei „Buchstaben“ gibt, doch je mehr verschiedene chemische Grund-Buchstaben existieren, umso komplexer werden die Decodierungs-Prozesse, weil die Vielzahl von „Buchstaben“ kompliziertere Erkennungs-Systeme erfordert. Für die Zell-Prozesse wurde die optimale Anzahl von 4 Buchstaben gewählt.
Es bleibt also die Frage: Wie viele Buchstaben der vier Grund-Buchstaben müssen kombiniert werden, um den Anforderungen zu entsprechen? Nehmen wir jeweils 2 der 4 Buchstaben und bilden ein „Wort“, so könnten wir insgesamt 4 mal 4 verschiedene solche „Worte“ bilden. Doch mit 16 verschiedenen Code-Worten könnten wir nicht alle 20 erforderlichen Aminosäuren codieren. Die folgende Tabelle zeigt einmal die 16 Möglichkeiten, die es gibt, jeweils 2 Buchstaben aus dem Vorrat von 4 Buchstaben (A, C, G, T) zu kombinieren, also Code-Worte aus 2 Buchstaben (2 Spalten der Tabelle) zu generieren.
Erst die Erweiterung der Wortlänge auf 3 Buchstaben bringt den Erfolg. Die Kombination von jeweils 3 Buchstaben aus dem Vorrat (A, C, G, T) erzeugt eine ausreichende Menge von verschiedenen „Worten“.
Mit der Wortlänge 3 ergibt sich die Gesamtmenge von 64 (d. h. 4³) möglichen Informationswerten. Es zeigt sich jedoch bei diesem Sprung von 16 auf 64, dass damit die Zielvorgabe von etwa 25 weit überboten wird (siehe Tabelle). Doch genau das ist im Sinne des Erfinders, weil, wie wir wissen, die Datensicherheit eine sehr hohe Priorität im System hat. Um diese zu erhöhen, werden alle Codierungen, die über die Zahl der benötigten 20 hinausgehen, redundant benutzt. Das heißt, dass einige Aminosäuren mehrfach codiert werden können. Damit werden viele potenzielle, operative oder vererbte Kopierfehler völlig wirkungslos und die Erkennungs-Systeme der Zelle für die Identifizierung einzelner Codons werden effizienter.
Für die Informations-Übertragung aus dem Zellkern zu den Lese-Synthesemaschinen (Ribosomen) wird die RNA, die sogenannte Messenger-RNA (mRNA), verwendet, die den Code der DNA aufnimmt, jedoch wird dabei anstelle des Thymin das Uracil (U) eingebaut. Die Prozesse der Informations-Übernahme aus der DNA in die mRNA sind sehr komplex und mehrstufig und werden in einem folgenden Abschnitt beschrieben.
Mit der Wortlänge 3 ergibt sich die Gesamtmenge von 64 (d. h. 4³) möglichen Informationswerten. Es zeigt sich jedoch bei diesem Sprung von 16 auf 64, dass damit die Zielvorgabe von etwa 25 weit überboten wird (siehe Tabelle). Doch genau das ist im Sinne des Erfinders, weil, wie wir wissen, die Datensicherheit eine sehr hohe Priorität im System hat. Um diese zu erhöhen, werden alle Codierungen, die über die Zahl der benötigten 20 hinausgehen, redundant benutzt. Das heißt, dass einige Aminosäuren mehrfach codiert werden können. Damit werden viele potenzielle, operative oder vererbte Kopierfehler völlig wirkungslos und die Erkennungs-Systeme der Zelle für die Identifizierung einzelner Codons werden effizienter.
Für die Informations-Übertragung aus dem Zellkern zu den Lese-Synthesemaschinen (Ribosomen) wird die RNA, die sogenannte Messenger-RNA (mRNA), verwendet, die den Code der DNA aufnimmt, jedoch wird dabei anstelle des Thymin das Uracil (U) eingebaut. Die Prozesse der Informations-Übernahme aus der DNA in die mRNA sind sehr komplex und mehrstufig und werden in einem folgenden Abschnitt beschrieben.
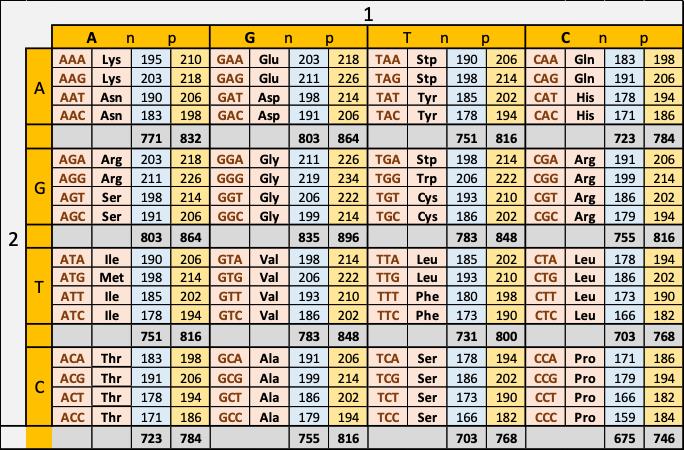
Di obige Tabelle enthält alle Aminosäuren und in den jeweils beiden Spalten rechts daneben die Anzahlen der Neutronen und Protonen, die zu ihrem Aufbau erforderlich sind.
